Acasă Blog~~Ghid detaliat pentru adaos complet~~

~~pe 2024/05/10~~ ~~597~~

Ghid detaliat pentru adaos complet

Pe tărâmul electronicelor digitale și al ingineriei informatice, adăugătoarele reprezintă unul dintre cele mai esențiale blocuri de construcție, pivotante în construcția și funcționalitatea circuitelor aritmetice mai complexe.Ca componente integrale ale unității de logică aritmetică (ALU), addrii facilitează numeroase operații de calcul, de la aritmetică de bază la sarcini logice complexe necesare pentru operațiunile sistemului.Proiectarea lor, care poate varia de la jumătăți simple, până la adăugări complete mai complexe, joacă un rol crucial în îmbunătățirea eficienței și vitezei de procesare în cadrul sistemelor digitale.Acest articol se încadrează în arhitectura detaliată și nuanțele funcționale ale diferitelor tipuri de adatori, ilustrând rolul lor critic în tehnologia modernă de calcul și explorarea logicii, circuitelor și aplicațiilor lor operaționale în contextul mai larg al designului logicii digitale.

Catalog

1. Ce este un adaos?

2. Jumătate de adaos

3. Adăugare completă

4. Tabelul de adevăr complet de adunare

5. Ecuațiile caracteristice ale unui adaos complet

6. Implementarea unui circuit complet de adunare

7. Avantaje și dezavantaje ale adaosurilor complete

8. Aplicații de adaosuri complete în logica digitală

9. Exemple de implementări complete de adunare

10. Concluzie

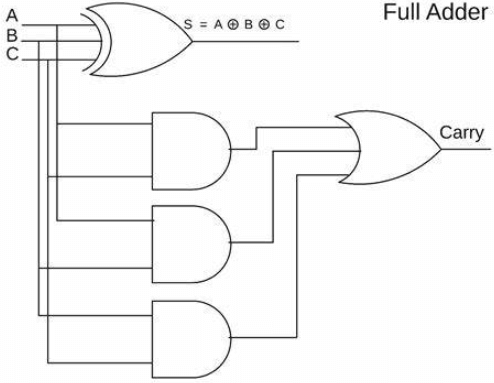
Figura 1: Adăugare completă

Ce este un adaos?

Un adaos este o componentă fundamentală în inginerie electronică și proiectarea logicii digitale și joacă un rol central în sistemele informatice mai complexe.Ca parte a unității logice aritmetice (ALU), adaosul gestionează o varietate de sarcini esențiale de calcul.Eficiența și performanța întregului procesor sunt afectate direct de proiectarea și funcționalitatea adaosului.

În procesor, adaosul este utilizat nu doar pentru operațiuni aritmetice de bază, cum ar fi adăugarea și scăderea, dar se angajează și într -o gamă mai largă de operații logice.De exemplu, atunci când rulează programe, procesorul trebuie adesea să calculeze noi adrese de memorie.Acest lucru se face de obicei prin adăugarea sau scăderea de la adresa curentă - o sarcină întreprinsă de adaos.Acestea controlează numărul de iterații de buclă și fluxul general prin creșterea și declinarea contoarelor.În aplicații mai complexe, cum ar fi indexarea tabelului, ADDER -urile localizează rapid datele calculând compensările.Acest lucru este important pentru sistemele de gestionare a bazelor de date, construcția compilatoarelor și procesarea datelor pe scară largă.Adăunurile sunt, de asemenea, esențiale în implementarea anumitor tehnici de mapare în sisteme de cache pe mai multe niveluri, folosind operații aritmetice pentru a determina poziția datelor în cache, optimizând astfel eficiența accesului.

Din punct de vedere tehnologic, adaosurile sunt implementate prin diferite proiecte de circuit, inclusiv adaosuri paralele, seriale și conducte.Adăugările paralele sunt favorizate pentru capacitatea lor de a gestiona simultan mai multe cifre, ceea ce le face potrivite pentru scenarii care necesită calcul rapid.Adatorii de serie, pe de altă parte, prelucrează un bit pe ciclu de ceas și sunt ideale pentru medii limitate de resurse sau cu putere mică.Adaosurile de conducte împart procesul de adăugare în mai multe etape, fiecare gestionând o parte din operația de adăugare.Acest design crește semnificativ viteza de calcul, în special în mediile de calcul performante.

Jumătate adaos

Un circuit pe jumătate de adăugare este un bloc fundamental în electronice digitale, special conceput pentru a adăuga două cifre binare unice.Acest circuit constituie fundamentul unui adaos complet și este esențial pentru înțelegerea proiectelor de circuit logice mai complexe.Într -o jumătate de adaos, există două intrări primare, etichetate A și B, care reprezintă Agend, respectiv adiția.Această configurație îi permite să calculeze suma și să transporte ieșirea fără a fi nevoie de o intrare de transport din calculele anterioare.

Nucleul unei jumătăți de adăugare este format din două porți logice: o poartă Xor și o poartă.Poarta Xor este responsabilă de generarea producției de sumă.Funcționează sub o regulă simplă în care iese un 1 dacă doar una dintre intrările sale este 1;În caz contrar, iese un 0. și poarta, pe de altă parte, se ocupă de ieșirea de transport.Produce un 1 numai atunci când ambele intrări ale acesteia sunt 1, aliniază perfect cu cerințele fundamentale ale adăugării binare.

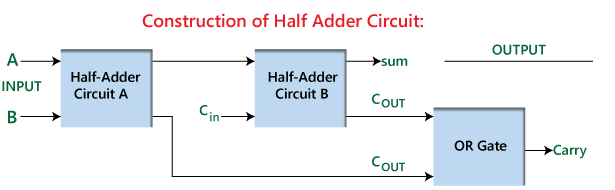
Figura 2: Construcția de jumătate de adaos

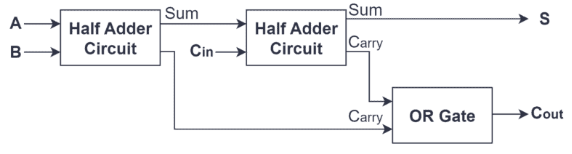
Acest design eficient și simplu permite jumătății de adunare nu numai să efectueze o adăugare binară de bază în mod independent, ci și să servească ca bloc de construcții pentru crearea unui adaos complet.Un adaos complet este construit prin combinarea a două jumătăți de adunări cu o poartă suplimentară sau suplimentară.În această configurație, prima repriză preia sarcina inițială de adăugare, generând o sumă preliminară și transport.A doua repriză de adunare procesează apoi transportul de la prima împreună cu o intrare suplimentară de transport.În cele din urmă, poarta OR îmbină cele două ieșiri de transport pentru a produce ieșirea finală de transport.Acest aranjament îmbunătățește funcționalitatea adaosului, permițându-i să se ocupe de sarcini mai complexe de adăugare pe mai multe biți, prezentând aplicarea pe scară largă și importanța jumătății de adatori în proiectarea circuitului digital.

Adăugare completă

Un adaos complet este o componentă avansată în designul logic digital, echipat pentru a gestiona adăugarea a trei intrări binare cu un singur bit, etichetate în mod obișnuit ca A, B și Carry-in (CIN).Acest design permite adăugarea completă pentru a prelucra eficient adăugările binare complexe prin încorporarea transportului de la calculele anterioare de ordin inferior într-o singură operație.

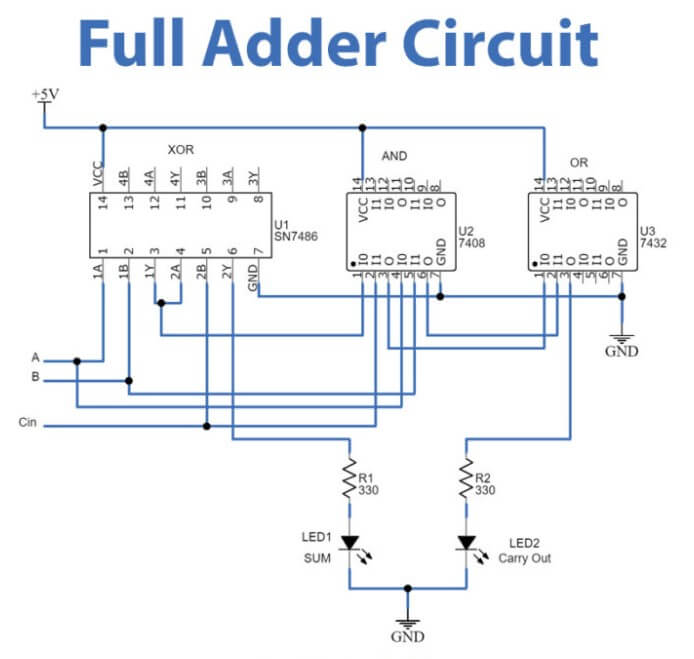
Figura 3: Circuit complet de adunare

Funcțional, un adaos complet poate produce o sumă din două cifre, ceea ce înseamnă că producția sa poate varia de la 0 la 3 și poate produce, de asemenea, un efect (COUT).Acest lucru se întâmplă deoarece, atunci când toate biții de intrare sunt setate la 1 (a = 1, b = 1, CIN = 1), ieșirea sumei va fi 1 (reprezentând binar 01) și se generează o derulare de 1, ceea ce indică faptul căO transport suplimentar trebuie să fie transmis la următorul bit mai mare.

Din punct de vedere structural, adaosul complet este format în general din două jumătăți de aduner și unul sau poartă.Prima repriză primește intrări A și B, generând o sumă inițială și un semnal de transport.Această sumă inițială este apoi alimentată, împreună cu transportul (CIN), în a doua jumătate de adăugare.Rolul a doua repriză este de a adăuga această sumă de la prima jumătate a lui Cin, producând o altă sumă și o nouă producție de transport.Simultan, ieșirea de transport din prima jumătate a adunărului și ieșirea de transport din a doua repriză sunt contopite printr-o poartă sau culminând cu efectul final (cout) al adăugării complete.Proiectarea acestei structuri asigură că adaosul complet gestionează eficient propagarea operațiunilor de transport în plus, ceea ce o face ideală pentru executarea adaosurilor binare pe mai multe biți.Astfel, proiectarea completă a adăugatului nu numai că accelerează prelucrarea datelor și îmbunătățește eficiența, dar simplifică complexitatea implementării hardware printr-o combinație simplă de porți logice, ceea ce o face o componentă indispensabilă în adăugarea cu mai multe cifre și unitatea logică aritmetică (ALU)

Parametri	Jumătate adaos	Adăugare completă
Descriere	Jumătate de adaos este o logică combinațională Circuit care adaugă două cifre de 1 biți.Jumătatea de adăugare produce o sumă dintre cele două intrări.	Un adaos complet este o logică combinațională Circuit care efectuează o operație de adăugare pe trei numere binare cu un biți. Adăugarea completă produce o sumă a celor trei intrări și valorile de transport.
Transport anterior	Carry anterior nu este utilizat.	Se folosește transportul anterior.
Intrări	În jumătate de adaos, există două biți de intrare (a, B).	În completare, există trei biți de intrare (A, B, C_în)
Ieșiri	Producția generată este de doi biți-sumă și transportați de la intrare de 2 biți.	Producția generată este de doi biți-sumă și transportați de la 3 biți.
Folosit ca	Un circuit pe jumătate de adăugare nu poate fi utilizat în La fel ca un circuit cu adăugare completă.	Un circuit complet de adunare poate fi utilizat pe loc dintr -un circuit pe jumătate de adunare.
Caracteristică	Este simplu și ușor de implementat	Designul unui adaos complet nu este la fel de Simplu ca o jumătate de adaos.
Expresie logică	Expresia logică pentru jumătate de adaos este: S = a⊕b;C = a*b.	Expresia logică pentru adaosul complet este: S = a⊕b⊕cin;C._afară= (ab)+(c_în(a⊕b)).
Porți logice	Este format dintr-o fostă poartă și una și Poartă.	Este format din două fost sau două și porți, și una sau poartă.
Aplicații	Este utilizat în calculatoare, calculatoare, Dispozitive de măsurare digitală etc.	Este utilizat în completări multiple de biți, procesoare digitale etc.
Nume alternativ	Nu există un nume alternativ pentru jumătate sumator.	Un adaos complet este cunoscut și sub numele de ondulare sumator.

Diagramă 1: Diferența dintre jumătatea adaosului și adaosul complet

Tabelul de adevăr complet de adunare

Tabelul de adevăr al unui adaos complet este cheia pentru înțelegerea logicii sale operaționale, detaliat relația precisă dintre combinațiile de intrare binară și rezultatele corespunzătoare ale acestora.Acest tabel demonstrează toate scenariile potențiale de intrare și rezultatele acestora, ceea ce îl face un instrument esențial în proiectarea și verificarea circuitelor logice digitale.Adăugarea completă procesează trei intrări: A, B și A transport (CIN), fiecare dintre ele fiind fie 0 sau 1. Aceasta duce la opt combinații posibile de intrări.

Pentru fiecare dintre aceste combinații, ieșirile din adaosul complet includ o sumă (sumă) și o transport (cout).Suma este adăugarea modulo-2 (operația XOR) a celor trei intrări-A, B și CIN.Realizarea are loc atunci când cel puțin doi dintre biți de intrare sunt 1. Aceasta reflectă capacitatea completă a adderului de a gestiona reportul în operațiuni de adăugare secvențială, asigurând precizia în calcule cu bit mai mare.

Pentru a ilustra, luați în considerare scenariul de intrare în care toate intrările sunt 0 (a = 0, b = 0, c-in = 0).Suma de ieșire va fi 0, iar transportul va fi, de asemenea, 0, ceea ce indică faptul că nu există o sumă suplimentară sau transportul de gestionat.Dacă un singur bit de intrare este 1, cum ar fi A = 1, B = 0, C-IN = 0, suma de ieșire va fi 1 fără transport, arătând că nu este nevoie să transferați o transport la un bit mai mare.Când doi biți de intrare sunt 1, ca a = 1, b = 1, c-in = 0, suma de ieșire este 0 (deoarece 1+1 este egal cu 2 în binar, iar modulo-2 rezultă în 0), dar transportul-Out este 1, indicând o transport care trebuie să fie transmisă la următorul bit mai mare.Cel mai complex scenariu apare atunci când toate cele trei biți de intrare sunt 1 (a = 1, b = 1, c-in = 1);Suma de ieșire este de 1 și există o derulare a 1, ceea ce sugerează că gestionarea transportului poate fi, de asemenea, necesară la biți și mai mari.

O	B	C._în	S	C._afară
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Graficul 2: Tabelul de adevăr complet de adunare

Caracteristici ecuații ale unui adaos complet

Înțelegerea completării complete implică disecția funcționalității sale folosind tabelul de adevăr, unde diferite combinații de valori de intrare A, B și C-in conduc la ieșiri sumă și cout.Pentru a înțelege operația, simplificăm ecuațiile logice pas cu pas.

Expresie logică pentru sumă

Ecuația începe cu cazurile distincte în care suma este egală cu 1:

• A 'B' CIN + A 'B CIN' + A B 'CIN' + AB CIN

Această ecuație poate fi condensată prin gruparea termenilor cu și fără CIN:

• CIN (A 'B' + AB) + CIN '(A' B + A B ')

Această simplificare duce la o formă mai ușor de implementat:

• Cin Xor (A Xor B)

Această reprezentare arată că producția de sumă este, în esență, operația XOR între A, B și CIN, captând comportamentul principal al adăugării binare în care suma comută pe baza unui număr ciudat de altele.

Logică pentru cout

Începând cu condițiile în care se generează transportul:

• A 'B CIN + A B' CIN + AB C-IN ' + AB CIN

Simplificarea ecuației, identificăm termeni care implică în mod obișnuit generarea unei transporturi:

• AB + B CIN + A CIN

În căutarea unei alte metode de implementare a coutului, ecuația poate fi reorganizată:

• AB + A CIN + B C-IN (A + A ')

Acest lucru se extinde și se recombină pentru a capta toate scenariile în care cel puțin două intrări sunt 1:

• AB CIN + AB + A C-IN + A 'B CIN

• AB (1 + CIN) + A C-IN + A 'B CIN

• AB + A C-IN (B + B ') + A' B CIN

• AB + A B 'CIN + A' B CIN

• AB + CIN (A 'B + A B')

Formularul compact final pentru cout:

• AB + CIN (A XOR B)

Această versiune a ecuației de realizare demonstrează modul în care cout este produs fie atunci când atât A, cât și B sunt 1, fie când unul dintre A sau B este 1 împreună cu un transport, încapsulând astfel logica necesară pentru gestionarea propagarea transportului în mai multe-Adăugare binară puțin.Această logică simplificată este deosebit de utilă pentru implementarea circuitelor digitale eficiente.

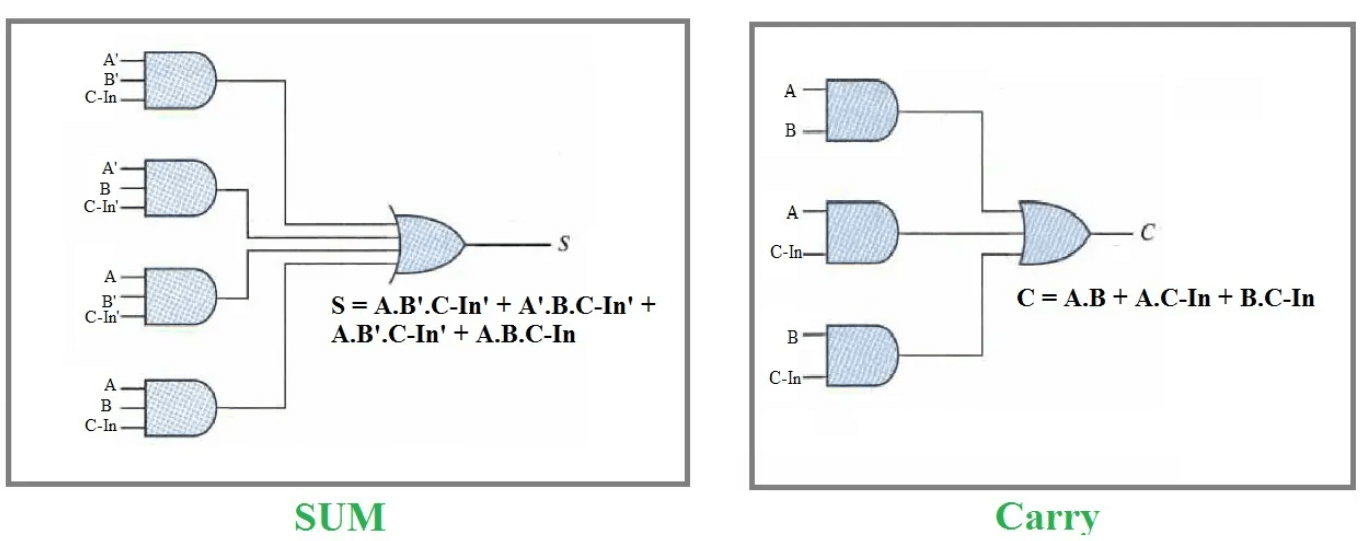
Figura 4: Ecuații ale unui adaos complet

Implementarea unui circuit complet de adunare

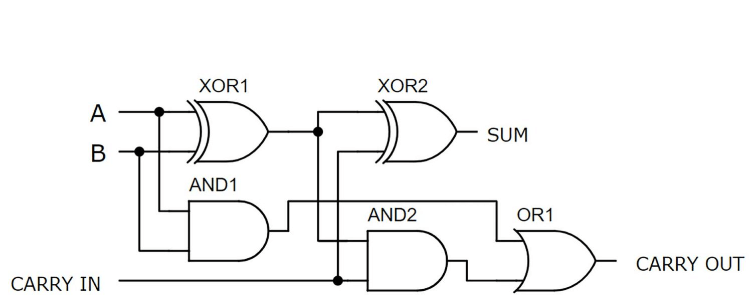
Implementarea unui circuit complet de adunare implică asamblarea cu atenție a două jumătăți de adaos și o poartă sau pentru a crea un dispozitiv capabil să gestioneze eficient adăugarea a trei intrări binare cu un singur bit.Acest aranjament optimizează complexitatea circuitului și asigură atât calcule eficiente, cât și exacte.

Pentru început, prima jumătate adaos ia două intrări binare primare, A și B, care sunt principalele cifre care trebuie adăugate.Sarcina sa cheie este de a calcula suma și reportul inițial al acestor două numere.Aici, prima repriză de adaos oferă două rezultate: o sumă inițială (suma1) și o transport inițială (Carry1).Suma1 este derivată din funcționarea XOR a A și B, ceea ce indică dacă totalul are un număr impar de 1.Carry1, rezultatul funcționării și între A și B, indică dacă ambele cifre sunt 1, necesitând o transport la următorul bit mai înalt.

În continuare, a doua repriză se alătură procesului.Utilizează suma de ieșire Sum1 și a treia CIN de intrare (transportul dintr-un calcul anterior) ca intrări.A doua repriză a adunării produce două ieșiri: rezultatul sumei finale (Sum2) și transportul secundar (Carry2).Sum2, care este rezultatul XOR al Sum1 și CIN, reprezintă suma finală a celor trei intrări, afișând adăugarea binară agregată.Carry2, care iese din funcționarea și operația dintre Sum1 și CIN, indică o reportare generată de aceste componente.

Full Adder Circuit with Using Two Half Adder

Figura 5: Circuit complet de adunare cu utilizarea a două jumătate de adaos

În cele din urmă, pentru a finaliza designul complet al adaosului, este necesară o poartă sau pentru a gestiona ieșirile de transport DRAY1 și transporta2 de la ambele jumătate de adunări.Aceasta sau poartă asigură că orice transport generat în timpul calculelor este transmis corect către ieșirea finală.Prin urmare, ieșirea finală de transport (COUT) a adaosului complet este sau rezultatul transport1 și transport2.Includerea acestei sau a poartă garantează că toate potențialele transporturi sunt calculate și transmise cu exactitate la nivelul următor în operațiuni de adăugare pe mai multe biți, asigurând integritatea operației aritmetice pe mai multe biți.

Avantaje și provocări ale adaosurilor complete în logica digitală

Adăugații complete joacă un rol indispensabil în proiectarea logicii digitale, oferind numeroase beneficii care le fac esențiale în diverse scenarii de calcul și prelucrare a datelor.Avantajele lor principale includ o flexibilitate remarcabilă, viteze de procesare rapidă și gestionarea eficientă a transportului.Aceste trăsături fac ca adăugătoarele complete ideale pentru executarea operațiunilor aritmetice complexe și a funcțiilor logice, în special în aplicațiile care necesită adăugare secvențială pe mai multe biți.

Avantaje

Flexibilitate: Adăugații complete excelează în capacitatea lor de a prelucra simultan mai multe intrări binare (A, B și CIN).De asemenea, pot fi extinse în tablouri de adunare mai mari pentru a gestiona numere binare mai lungi.Această scalabilitate este importantă pentru construirea de unități de logică aritmetică de înaltă performanță (ALUS), care trebuie să efectueze operațiuni aritmetice și logice complexe pe mai multe biți.

Viteză: Datorită arhitecturii lor interne de procesare paralelă, adaosurile complete pot completa adăugarea tuturor intrărilor într -un singur ciclu de ceas, determinând, de asemenea, să poarte ieșiri.Această capacitate acceptă operațiuni de adăugare continuă și este indispensabilă pentru procesarea datelor în timp real în microprocesoarele moderne și dispozitivele de calcul de mare viteză.

Dezavantaje

Cu toate acestea, ADDER -urile complete prezintă, de asemenea, dezavantaje notabile:

Complexitate în proiectare și implementare: Adatorii complete implică mai multe porți logice și propagarea transportului pe mai multe niveluri, ceea ce face ca designul lor să fie complex.Această complexitate nu numai că crește costurile de fabricație, dar poate afecta și fiabilitatea circuitelor.

Probleme de întârziere de propagare: Propagarea transportului poate trece prin mai multe porți logice, fiecare adăugându -și întârzierea.Acest lucru poate limita viteza de calcul generală în timpul operațiunilor la scară largă, în special în sisteme informatice extinse și în proiectarea integrării la scară largă (VLSI) și a procesoarelor de mare viteză.Întârzierea poate deveni un blocaj semnificativ în performanță.

Pentru a atenua aceste probleme, inginerii explorează continuu proiecte de circuit mai eficiente.Strategiile includ utilizarea tehnologiilor de poartă logică mai rapidă, optimizarea machetei circuitului pentru a scurta lungimile căilor și dezvoltarea de tehnologii avansate, cum ar fi adaosurile de salvare a transportului pentru a minimiza întârzierile în propagarea transportului.

Aplicații de adaosuri complete în logică digitală

Adăugările complete sunt utilizate pe scară largă în logica digitală, apreciate pentru flexibilitatea și eficiența lor, ceea ce le face centrale pentru o multitudine de sarcini de calcul și procesare a datelor.Aplicația lor se întinde de la operațiuni aritmetice de bază la procesarea complexă a semnalului și controlul sistemului.Iată o privire detaliată asupra unor domenii cheie în care adăugătoarele complete sunt integrale.

Circuite aritmetice

Una dintre cele mai simple utilizări ale adatorilor complete este în circuite aritmetice unde efectuează adăugare binară.Mai ales crucial în adăugarea numărului pe mai multe biți, adăugătorii complete gestionează secvențe binare mai lungi prin cascadă.În acest aranjament, fiecare adaos complet gestionează adăugarea pentru poziția sa de biți și transportul din bitul inferior, apoi trece noua transport la următorul bit mai mare.Această cascadă permite adăugarea completă pe mai multe biți pe întreaga gamă de cifre.

Prelucrarea datelor

Adatorii complete joacă, de asemenea, un rol esențial în sarcinile avansate de prelucrare a datelor, cum ar fi procesarea digitală a semnalului (DSP) pentru filtrare și transformările Fourier, unde sunt necesare operațiuni aritmetice precise și rapide.În plus, pe tărâmul securității informațiilor, inclusiv algoritmii de criptare a datelor și detectarea erorilor și corecția de corecție, cum ar fi verificările de paritate și generarea de cod de verificare a cicliei (CRC), addtorii complete sunt cruciale pentru executarea operațiunilor esențiale de biți.

Contoare

În contoarele digitale, adăugătoarele complete sunt indispensabile pentru implementarea atât a funcțiilor de creștere, cât și de decrement, în special în contoarele modulare și sincrone.Ei gestionează cu exactitate purtările și împrumuturile pentru a asigura numărarea precisă.

Multiplexers (MUX) și demultiplexers (demux)

În multiplexori și demultiplexori, adăugătorii complete joacă un rol critic în selecția canalelor și în distribuirea datelor.Ei participă la logica care determină ce canale sunt utilizate pentru introducerea și ieșirea datelor, luând decizii pe baza semnalelor de control logice.

Tehnologia memoriei

În adresarea memoriei, ADDER -urile complete ajută la generarea de semnale de adresă pentru accesarea dinamică a locațiilor de memorie.Acest lucru este deosebit de important în memoria dinamică cu acces aleatoriu (DRAM) și în alte sisteme de stocare, unde adăugătorii complete acceptă calcule complexe de adrese pentru a îmbunătăți eficiența accesului la memorie.

Unități logice aritmetice (ALU)

În cele din urmă, ca componente fundamentale ale unităților logice aritmetice în microprocesoare și procesoare de semnal digital, addtorii complete sunt cruciale.ALU se ocupă de toate operațiunile aritmetice și logice, cu adăugări complete asigurând procesarea datelor atât rapid, cât și exact.

Exemple de implementări complete de adunare

Adăugările complete pot fi construite folosind diverse porți și configurații logice.Aici, explorăm patru implementări diferite, subliniind configurarea și nuanțele operaționale.

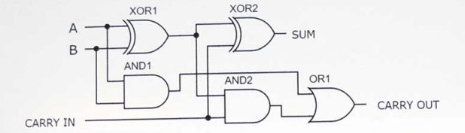
Adder complet construit cu Xor, și sau porți

Full Adder Built with XOR, AND, and OR Logic Gates

Figura 6: Adator complet construit cu Xor și, sau porți logice

Acest exemplu prezintă un adaos complet construit pe o bordură folosind tranzistoare discrete.Configurația cuprinde cinci porți logice: două porți XOR, două și porți și una sau poartă, necesitând un total de 21 de tranzistoare.Intrările A și B sunt conectate la stânga sus a plăcii, primind o alimentare +5V.Aceste intrări sunt controlate folosind două comutatoare de comutare.Două LED -uri din stânga sus indică stările de intrări A și B, în timp ce două LED -uri din partea dreaptă afișează ieșirile.Rezistențele utilizate în circuit sunt de 2,2k ohmi.Când intrările A și B sunt pornite și transportul este oprit, ieșirea arată o valoare binară de 10, reprezentând suma 2 (1 + 1 + 0 = 10).Porțile Xor, construite cu primele 12 tranzistoare, se ocupă de însumarea primară, în timp ce jumătatea inferioară a plăcii de pâine conține și și porțile pentru operațiuni de transport, cablarea codificată în culori îmbunătățește claritatea și depanarea.

Adăugare completă folosind Nand Gates

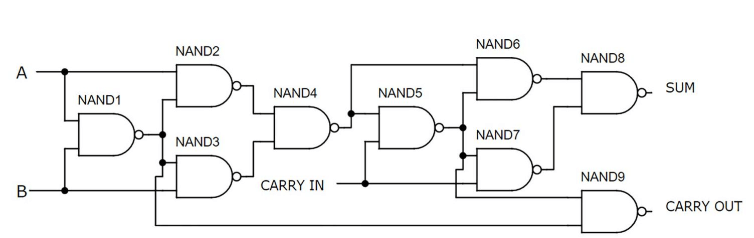
Figura 7: Adăugare completă folosind porți NAND

Acest adaos complet folosește nouă porți NAND, cu fiecare poartă realizată din două tranzistoare, în valoare totală de 18 tranzistoare.Această metodă este printre cele mai simple și mai eficiente moduri de a construi un adunare completă folosind componente discrete.Toate porțile sunt asamblate pe jumătatea superioară a plăcii de pâine, în timp ce întrerupătoarele ocupă jumătatea inferioară.Funcționalitatea circuitului este demonstrată cu intrările A și B ON și transportul Oprit, rezultând o valoare binară de ieșire de 10, echivalentă cu Decimalul 2.

Adaos complet cu nici porți

Figura 8: Adăugare completă cu nici porți

Construită cu nouă porți și nici cele care necesită două tranzistoare, această configurație folosește, de asemenea, 18 tranzistoare în total.Construirea unui adaos complet cu Nor Gates oferă o alternativă bună, dar implică cabluri mai complexe în comparație cu Nand Gates.Fiecare tranzistor din porți și nu este împământat, colecționarii conectați prin fire de jumper portocaliu pentru a asigura cablarea îngrijită și organizată.Această configurație este prezentată cu intrări A și B activate și transportul dezactivat, ceea ce duce la ieșirile în care transportul este activ și suma este oprită.

Concluzie

De -a lungul acestei explorări a tehnologiei de adunare, de la jumătăți de bază de bază la proiecte sofisticate complete de adunare, este evident că aceste componente sunt bazate pe avansarea electronicelor digitale.Caracteristicile operaționale și exemplele de implementare au oferit subliniază versatilitatea și eficiența adatorilor în diferite setări de calcul.Examinând structura și funcția addrilor, în special prin tabelele lor de adevăr și ecuațiile caracteristice, obținem informații valoroase asupra capacităților și constrângerilor lor.Această cunoaștere este esențială în promovarea proiectării unor sisteme de calcul mai eficiente și mai rapide.În cele din urmă, ADDER -urile nu numai că simplifică calcule binare complexe, dar permit și proliferarea tehnologiei în zone la fel de diverse precum prelucrarea datelor, alocarea memoriei și procesarea digitală a semnalului.Pe măsură ce tehnologia digitală evoluează, rafinarea și inovația continuă în proiectarea de adunare vor continua să fie o piatră de temelie în dezvoltarea arhitecturilor de calcul mai avansate, asigurându -se că aceste componente fundamentale rămân în centrul proiectării și implementării sistemului digital.

Întrebări frecvente [FAQ]

1. Ce este un circuit complet de adunare?

Un adaos complet este un circuit digital care adaugă trei biți binare pentru a produce o sumă și o producție de transport.Este conceput pentru a gestiona adăugarea a trei intrări: două biți semnificative și un bit de transport dintr-un plus anterior.Acest lucru îi permite să fie utilizat în etape succesive pentru a adăuga numere binare pe mai multe biți.

2. Câți și, sau, Xor în completare?

Un adaos tipic complet conține:

Două porți XOR pentru generarea sumei.

Doi și porți pentru a contribui la calculul efectuării.

Una sau poartă pentru a finaliza ieșirea de efect.

3. Ce este intrarea de transport în completare?

Intrarea de transport (CIN) într-un adaos complet este bitul de transport din adăugarea bițiilor semnificative anterioare mai mici în adăugarea binară pe mai multe biți.Permite că adăugarea completă să ia în considerare această reportaj anterior atunci când se calculează suma curentă și noua efect.

4. De ce să folosiți un adaos complet în loc de o jumătate de adaos?

Un adaos complet este utilizat în loc de o jumătate de adaos, deoarece poate adăuga trei biți (inclusiv transportul din completările anterioare), ceea ce îl face potrivit pentru înlănțuirea împreună pentru a adăuga numere cu mai multe biți.O jumătate de adăugare poate adăuga doar doi biți și nu are o prevedere pentru o transport, ceea ce limitează utilizarea sa la cele mai simple forme de adăugare binară fără propagarea secvențială a transportului.

Despre noi

ALLELCO LIMITED

Allelco este un un singur stop la nivel internațional Distribuitor de servicii de achiziții de componente electronice hibride, angajat să furnizeze servicii de achiziții de componente și lanțuri de aprovizionare complete pentru industria globală de fabricație și distribuție electronică, inclusiv fabrici de top 500 globale OEM și brokeri independenți.
Citeste mai mult